Harry Markowitz’s Modern Portfolio Theory: The Efficient Frontier

There’s no such thing as the perfect investment but crafting a strategy that offers high returns and relatively low risk is priority for modern investors. While this hallmark seems rather straightforward today, this strategy actually didn’t exist until the latter half of the 20th century.
Modern Portfolio Theory

In 1952, an economist named Harry Markowitz wrote his dissertation on “Portfolio Selection”, a paper that contained theories which transformed the landscape of portfolio management—a paper which would earn him the Nobel Prize in Economics nearly four decades later.
As the philosophical antithesis of traditional stock selection, his Modern Portfolio Theory (MPT) continues to be a popular investment strategy, and this portfolio management tool—if used correctly—can result in a diverse, profitable investment portfolio.
Instead of focusing on the risk of each individual asset, Markowitz demonstrated that a diversified portfolio is less volatile than the total sum of its individual parts. While each asset itself might be quite volatile, the volatility of the entire portfolio can actually be quite low.
More than 70 years after its introduction, the fundamentals of MPT ring true. Let’s delve into this popular portfolio management strategy and discover what makes the principles of this revolutionary theory so effective.
Harry Markowitz: The Man Behind MPT

Before we can examine the tenets of MPT, it’s important to understand the man behind it. Markowitz’s name is an institution in the financial realm; today, much of what governs modern financial and retirement saving advice is a result of his work.
Decades before he became a Nobel Laureate, Harry Markowitz built an illustrious career as an economist.
Born August 24th, 1927, in Chicago, Illinois, Markowitz showed interest in physics, astronomy, and philosophy early on, and displayed particular interest in the ideas of David Hume. He would continue to follow his interest in Hume’s ideologies throughout his undergraduate years at the University of Chicago. While still a student, Markowitz was invited to join the Cowles Commission for Research in Economics (now the Cowles Foundation at Yale University), at the time directed by T. Koopmans.
After receiving his bachelor’s degree, Markowitz continued his studies at the University of Chicago with a specialization in Economics. During his time there, Markowitz took classes under some of the most notable academics of the time, including Milton Friedman, Jacob Marschak, and Leonard “Jimmie” Savage.
In 1952, Markowitz joined the RAND Corporation, and in the same year, his article on “Portfolio Selection” was published in The Journal of Finance. While with RAND, he worked on a variety of simulation problems, and soon moved to General Electric. After leaving GE, Markowitz made his return to RAND for a second time.
While applied mathematics continued to progress, researchers lacked computer resources that could implement these new, groundbreaking ideas. Any time an analytical thinker wanted to examine a novel idea, they were tasked with writing unique pieces of computer code. This inspired Markowitz and his team to develop SIMSCRIPT, a powerful computer simulation language that allowed these researchers to take advantage of useful, reusable code. After departing RAND for the second time, Markowitz founded Consolidated Analysis Centers, Inc., where he and his team developed a proprietary, upgraded version of SIMSCRIPT that would eventually be sold publicly.
Today, Markowitz is both a professor and a consultant. As an adjunct professor at the Rady School of Management at the University of California at San Diego, Markowitz casts video lectures and consults out of his Harry Markowitz Company offices.

Listen to how Dr. Harry Markowitz believes financial advisors can help with market uncertainty and what he believes is a common mistake made by many when investing. This video may have been made in 2010, but the advice and information is timeless.
Awards and Accolades
Markowitz’s “Portfolio Selection” was published in 1952, but in the 70 years following, he’s continued to gain accolades and awards in regard to a variety of topics. His focus, however, has been the application of mathematical and computing techniques to practical problems—especially business decisions made under measures of uncertainty.
During his tenure as a professor of finance at Baruch College of the City University of New York, in 1990, he won the Nobel Memorial Prize in Economic Sciences for MPT.
The following year, he received the John von Neumann Theory Prize from the Operations Research Society of America (now Institute for Operations Research and the Management Sciences, INFORMS) for his contributions in the theory of three fields: portfolio theory, sparse matrix methods, and simulation language programming (SIMSCRIPT).
Pensions and Investments Magazine also named Harry Markowitz as “Man of the Century”. Markowitz is one of the brilliant minds behind GuidedChoice. As co-founder and Chief Architect, his theory has informed the backbone of our proprietary investment model.
The Origins of MPT
In pursuit of his Ph.D., Markowitz wrote his dissertation on the application of mathematics in the analysis of the stock market. While completing his research, Markowitz noticed shortcomings in the then-current understanding of stock prices.

According to Markowitz’s own account, the basic concepts of what would become MPT came to him while reading a passage from John Burr Williams’ Theory of Investment Value. Prior to the development of MPT, investing processes were centered on individual stocks; investors would look through available assets and find “sure bets”—assets that would produce decent returns without subjecting the investor to too much risk. Expected net present value (NPV) was used to distinguish these “sure bet” stocks, while securities were valued by discounting their future cash flows. Stocks that were capable of generating more money at a quicker rate were given great value.
Markowitz disagreed with this thinking. The “present value” theory had shortcomings; selecting the “best” portfolio under this logic meant selecting a single stock with the highest expected NPV. That approach was risky by nature, and while economic experts believed a good portfolio was a diversified one, there was no methodology available for investors to achieve this diversity.
Markowitz looked to probability and statistics to further his insights; if one believed a stock’s price changed randomly, statistical tools including mean and variance could be used to form more diverse portfolios. In the instance of two or more stocks, an investor could consider correlation.
What is MPT?
Markowitz created a formula that allows an investor to mathematically trade off risk tolerance and reward expectations, resulting in the ideal portfolio.
This theory was based on two main concepts:
1. Every investor’s goal is to maximize return for any level of risk
2. Risk can be reduced by diversifying a portfolio through individual, unrelated securities
MPT works under the assumption that investors are risk-averse, preferring a portfolio with less risk for a given level of return. Under this assumption, investors will only take on high-risk investments if they can expect a larger reward.
Consider the following example:
A “rational investor” is asked to choose between two investments: Investment A and Investment B. Both are expected to increase in value by six percent each year. However, Investment B is considered twice as volatile as Investment A, meaning its value fluctuates at twice the magnitude of Investment A’s value fluctuations.
MPT suggests that a rational investor will always choose the less volatile asset, in this case Investment A, so long as both options provide an equivalent expected return.
A portfolio’s overall risk is computed through a function of the variances of each asset, along with the correlations between each pair of assets. Asset correlations affect the total portfolio risk, formulating a smaller standard deviation than would be found by a weighted sum.
With these insights, Markowitz worked to create a management system that would transform the landscape of modern investing processes and published his new theory in The Journal of Finance in 1952.
Under MPT—or mean-variance analysis—an investor can hold a high-risk asset, mutual fund, or security, so long as this high-risk investment is minimized by all underlying assets. The portfolio itself is balanced in a way that its overall risk is lower than some of its underlying investments. Risk is defined as the range by which an asset’s price will vary on average, but Markowitz split risk into two subsequent categories.
Two Components of Risk
According to MPT, there are two components of risk for individual stock returns.
In a truly diversified combination of assets—or portfolio—the risk of each asset itself contributes very little to overall portfolio risk. Rather, the covariances among the individual assets determine more of the overall portfolio risk.
Therefore, investors can reduce individual asset risk by combining a diversified portfolio of assets.
1. Systematic Risk
This refers to market risks that cannot be reduced through diversification, or the possibility that the entire market and economy will show losses that negatively affect investments. It’s important to note that MPT does not claim to be able to moderate this type of risk, as it is inherent to an entire market or market segment.
2. Unsystematic Risk
Also called specific risk, unsystematic risk is specific to individual stocks, meaning it can be diversified as you increase the number of stocks in your portfolio.
The Efficient Frontier
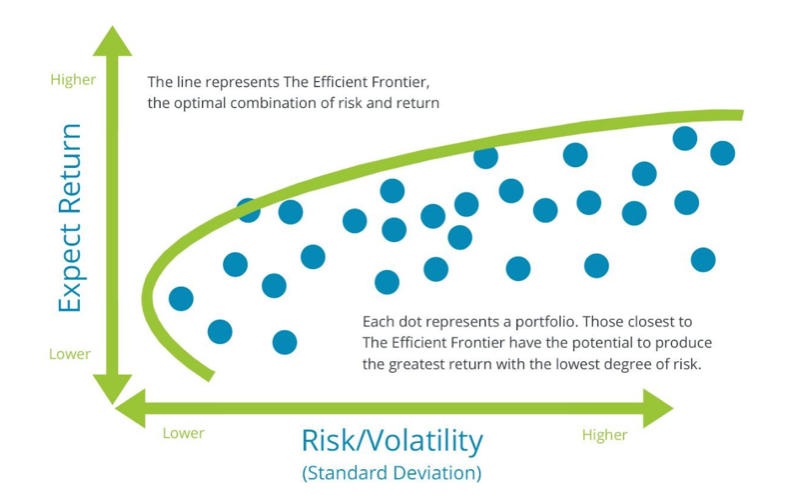
While the benefits of diversification are clear, investors must determine the level of diversification that best suits them. This can be determined through what is called the Efficient Frontier, a graphical representation of all possible combinations of risky securities for an optimal level of return given a particular level of risk.
- At every level of return, investors can create a portfolio that offers the lowest possible risk.
- For every level of risk, investors can create a portfolio that offers the highest return.
Any portfolio that falls outside the Efficient Frontier is considered sub-optimal for one of two reasons: it carries too much risk relative to its return, or too little return relative to its risk. A portfolio that lies below the Efficient Frontier doesn’t provide enough return when compared to the level of risk. Portfolios found to the right of the Efficient Frontier have a higher level of risk for the defined rate of return.
At every point on the Efficient Frontier, investors can construct at least one portfolio from all available investments that features the expected risk and return corresponding to that point. A portfolio found on the upper portion of the curve is efficient, as it gives the maximum expected return for the given level of risk.
The Efficient Frontier offers a clear demonstration of the power behind diversification. There’s no singular Efficient Frontier, because investors can alter the number and characteristics of the assets to conform to their needs.
Why Many Misunderstand MPT
When it comes to information about MPT, confusion abounds. Many confuse MPT with the Capital Asset Pricing Model (CAPM). Others confuse how they may have experienced MPT with its actual assumptions.
CAPM builds on MPT, but it makes several unrealistic assumptions, including:
| CAPM Assumptions | MPT |
|---|---|
| All investors share the same expectations. | Use your own assumptions for your own purposes. |
| Investors may borrow at the risk-free rate. | Use realistic assumptions. |
| There is only one source of expected return, that of the global capital market portfolio. All other apparent sources are spurious and should be diversified away. | Apply MPT using any reasonable set of return assumptions you believe are relevant. |
| For a person saving for retirement, the assumptions might pertain to asset classes. | |
| For an equity portfolio manager seeking to beat a benchmark, they might instead pertain to sources of extra return (a.k.a. “alpha”), such as Value, Size, Momentum, Earnings Quality, or Low Volatility. | |
| This versatility is why MPT is embedded in so many investment software applications: its framework is generic enough to be useful to different parties seeking to achieve different goals. |
Other Sources of Confusion
Too often, persons confuse how they experienced MPT being applied with how it is meant to be applied.
| Confused Beliefs | MPT |
|---|---|
| Believes using standard deviation as the risk measure means it assumes all investment returns are normally distributed, when in fact they are not. | Makes no assumption about the shape of return distributions. |
| Believes standard deviation is a bad risk measure because it punishes “upside risk.” | MPT allows for using “downside risk” measures instead. The 1959 book, Portfolio Selection, has an entire chapter titled “The Semi-variance.” |
| Believes MPT requires using sample historical data over some recent period, as-is, as the MPT inputs. | MPT recommends you consider as much data as possible and use judgment when making assumptions. |
| An obvious example of this being illogical for return expectations is that bond returns rise when bond yields fall. It seems unreasonable to expect the same high returns in the future when starting from a lower yield. | MPT is silent on exactly how to develop return assumptions, other than to use judgment, preferably that of a knowledgeable investor. |
| An example of this being illogical for risk expectations is after a benign return period. For example, based only on the period 2012 – 2017, you could never predict such stressful periods as the 1987 crash or the 2008 global financial crisis. | By using as much data as possible (which for many asset classes, dates back to the early 20th and sometimes the 19th century), you would never be surprised that crashes occur. |
| Which information is relevant is different for different investors. A highly leveraged hedge fund might care only about the next day, week, or quarter, and might shift its risk assumptions very frequently. But an investor saving for retirement cares about the next several decades and might shift investment assumptions very rarely. |
In 2008, the stock market unexpectedly plunged almost 40 percent. Did MPT hold up during that financial crisis? Yes, because the theory itself predicts it.
Does MPT Work in Recessions?
As asset classes go down, correlations tend to increase. Historically, asset classes shift proportionally to their betas. The beta measures how risky an individual security is in relation to the overall stock market. Consider an asset with a beta value of 1. In the event of a market decline, any stock that has a beta value greater than 1 stands to lose more money than a stock with a beta value less than 1.
So how did this play out in the Great Recession of 2008? According to Markowitz, investors that limited risk during the recession kept a percentage of their portfolios in lower-risk U.S. Treasury bonds; these investments were top performers, while stocks and corporate bonds took a dive.

Using MPT for Retirement Investing
Trillions of dollars in institutional assets are invested under the tenets laid out by MPT. This financial tool permits a financial or retirement advisor to create a client’s optimal portfolio by balancing risk and return.
Once you’ve informed your adviser about the level of risk you’re comfortable with, he or she can construct a portfolio using MPT that maximizes the expected return for the defined risk.
Investors who diversified their portfolios still saw a loss, but a significantly smaller loss than investors who didn’t.
Ultimately, using MPT for your portfolio management is dependent on your desires as an investor. If you’re looking for greater return on average, you’ll have to accept greater risk. If you want to incur fewer month-to-month or year-to-year fluctuations, you’ll have to accept less return over time. Either way, MPT can identify the optimal allocation of assets according to your preference.
